El Fascinante Mundo de los Ángulos: Clasificación, Propiedades y Ejercicios

Introducción

¡Bienvenidos, amantes de la geometría, a un emocionante recorrido por el mundo de los ángulos! ¿Sabías que los ángulos son piezas fundamentales en la construcción de figuras geométricas? Desde los majestuosos triángulos hasta los versátiles cuadriláteros, los ángulos dan forma y estructura a nuestro universo matemático. Pero eso no es todo, los ángulos también se esconden en la vida cotidiana, en el arte, la arquitectura e incluso en la naturaleza.

En este artículo, exploraremos los diferentes tipos de ángulos, sus propiedades y cómo se relacionan entre sí. Aprenderemos a medirlos utilizando el sistema sexagesimal y descubriremos conceptos clave como la bisectriz, la perpendicularidad y la mediatriz. Prepárate para desentrañar los secretos de los ángulos y dominar esta fascinante rama de la geometría.

El Rayo Geométrico: El Punto de Partida

Antes de sumergirnos en los ángulos, debemos conocer su componente básico: el rayo geométrico. Imagina una línea recta que se extiende infinitamente en ambas direcciones. Ahora, selecciona un punto en esa línea y divídela en dos partes. Cada una de estas partes es un rayo geométrico, que se origina en el punto y se extiende en una sola dirección.

Definición: Un rayo geométrico es una sección de la recta que se genera cuando esta es dividida a partir de uno de sus puntos, prolongándose únicamente en una dirección y conteniendo solamente a todos los puntos que están en esa dirección.

Notación de los rayos geométricos

En el siguiente gráfico la recta m es dividida en dos partes por el punto O extendiéndose el rayo en dirección hacia el punto A . Para describir este rayo se utilizará la siguiente notación : $\overrightarrow{OA}$ o bien $\overleftarrow{AO}$, es decir: $\overrightarrow{OA}=\overleftarrow{AO}$. Al punto O se le llama vértice u origen.


La recta m es dividida por el punto O, avanzando el rayo en dirección hacia A.

No confunda el rayo $\overrightarrow{OA}$ con el rayo $\overrightarrow{AO}$ ; (la flecha en la parte superior indica el origen y dirección del rayo). Note que tienen diferente origen y dirección, aunque ambos son parte de la misma recta, en consecuencia: $\overrightarrow{OA}\neq\overrightarrow{AO}$
Observe esta diferencia en los siguientes gráficos:

$\overrightarrow{OA}$

$\overrightarrow{AO}$

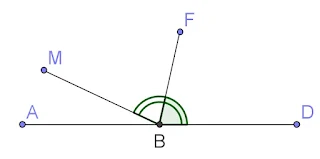
Los Ángulos: Encuentro de Rayos

Cuando dos rayos comparten el mismo punto de origen, forman un ángulo. Este punto de origen se llama vértice, y los rayos se conocen como lados del ángulo.

Definición: Un ángulo es la figura geométrica que se forma cuando se trazan dos rayos desde el mismo origen. Al origen se lo llama vértice y los rayos lados.

En la siguiente figura el rayo $\overrightarrow{OB}$ y el rayo $\overrightarrow{OA}$ tienen como origen el punto $O$. El punto $O$ es el vértice del ángulo.

El ángulo $\angle{BOA}$

Elementos de un ángulo

Un ángulo posee las siguientes partes:

- Dos rayos: $\overrightarrow{OB}$ y $\overrightarrow{OA}$

- El vértice: El punto $O$

Notación de los ángulos

Para nombrar un ángulo se emplea cualquiera de las siguientes notaciones:

Utilizando tres puntos (uno de cada rayo y el vértice), debe observar que cuando se emplea esta notación el vértice siempre va al medio. Ejemplo: $\angle{BOA}=\angle{AOB}=\widehat{AOB}=A\widehat{O}B$

Utilizando únicamente el vértice del ángulo, por ejemplo: $\angle{O}=\widehat{O}$.

Utilizando la amplitud del ángulo, en este caso debe utilizar el alfabeto griego, siendo común emplear las letras: $\alpha, \beta, \gamma, \theta$.

Diferentes formas de nombrar un ángulo

Midiendo Ángulos: El Sistema Sexagesimal

Para medir la amplitud de un ángulo, utilizamos el sistema sexagesimal, que divide una circunferencia en 360 grados (°). Cada grado se subdivide en 60 minutos (') y cada minuto en 60 segundos ("). Esta escala nos permite medir con precisión la abertura de cualquier ángulo.

Este sistema lo que busca es medir la amplitud del ángulo, para ello se estructura la siguiente escala de medición: Consideramos una circunferencia de centro $O$ ( el centro $O$ será el vértice del ángulo) y la dividimos en 360 partes iguales. Cada una de estas partes de la circunferencia representa un grado(°).

Circunferencia dividida en 360 partes iguales

Medir los grados

Haciendo coincidir el vértice del ángulo en el centro de la circunferencia; y ubicando los rayos adecuadamente, podemos contar cuantos grados de amplitud tiene el ángulo.

El ángulo $\angle{AOB}=40°$

Medir los minutos

Un grado (°) se divide en 60 partes, cada una de estas partes representa un minuto ('), en consecuencia $1°=60'$. Por lo que en un grado (1°) entran sesenta minutos (60').

Medir los segundos

Si un minuto (') se divide en 60 partes, cada una de estas partes equivale a un segundo (''), en consecuencia, $1'=60''$.

Relación entre grados, minutos y segundos

La relación entre grados, minutos y segundos es la siguiente:
$1°=60'$
$1'=60''$
$1°=60'=3600''$

Igualdad de Ángulos: Mismo Valor, Diferente Apariencia

En geometría, dos ángulos son iguales si tienen la misma medida, es decir, si abarcan la misma porción de un círculo. Esto puede parecer obvio, pero es importante destacar que la apariencia de los ángulos puede variar significativamente.

Definición: Dos ángulos son iguales si tienen la misma medida.

Observa los siguientes ángulos y notaras que tienen la misma amplitud. En consecuencia los tres ángulos son iguales, es decir: $\angle{DEF}= \angle{IHG}=\angle{ABC}= 30°$.
El tamaño de los rayos no influye en la medida del ángulo ya que estos pueden extenderse indefinidamente.

$\angle{DEF}=30°$

$\angle{IHG}=30°$

$\angle{ABC}=30°$

¿Cómo Saber si Dos Ángulos son Iguales?

La forma más sencilla de determinar si dos ángulos son iguales es medirlos con un transportador. Si ambos ángulos tienen la misma medida en grados, minutos y segundos, entonces son iguales.

Ángulos Iguales en Diferentes Posiciones y Tamaños

Es fundamental comprender que la igualdad de ángulos no depende de su posición ni del tamaño de sus lados. Dos ángulos pueden estar orientados de manera diferente o tener lados de distinta longitud, pero seguir siendo iguales si sus medidas son las mismas.

Imagina dos porciones de pizza cortadas con el mismo ángulo. No importa si una porción es más grande que la otra o si están giradas de manera diferente; el ángulo de corte sigue siendo el mismo.

En los gráficos, a menudo se marcan los ángulos iguales con la misma seña. Esto ayuda a visualizar rápidamente qué ángulos tienen la misma medida.

Tipos de Ángulos: Una Variedad de Formas

Los ángulos vienen en todas las formas y tamaños, y se clasifican según su amplitud y su relación con otros ángulos.

Tipos de Ángulos Según su Amplitud

La clasificación de los ángulos según su medida nos lleva a descubrir una variedad de formas:

Ángulo nulo: Mide 0°.
Ángulo agudo: Mide más de 0° y menos de 90°.
Ángulo recto: Mide exactamente 90°.
Ángulo obtuso: Mide más de 90° y menos de 180°.
Ángulo llano: Mide 180°.
Ángulo de giro: Mide 360°.

Clasificación de los ángulos segun su amplitud

Ángulo nulo: Un ángulo nulo es aquel cuya medida es igual a 0°

El $\angle{AOB}= 0°$, por tanto es un ángulo nulo

Ángulo agudo: Un ángulo agudo es aquel cuya medida es mayor a 0° y menor a 90°

El ángulo $\alpha$ es agudo
porque es mayor a 0° y es menor a 90°, es decir: $0°<\alpha<90°$

Ángulo recto: Un ángulo recto es aquel cuya medida es igual a 90°

El $\angle{B}$ es un ángulo recto porque $\angle{B}=90°$

Ángulo obtuso: Un ángulo obtuso es aquel cuya medida es mayor a 90° y menor a 180°

El $\angle{BAD}$ es un ángulo obtuso porque es mayor a 90° y menor a 180°,
es decir: $$0°<\angle{BAD}<180°$$

$\theta$ es un ángulo obtuso porque es mayor a 90° y menor a 180°, es decir: $$0°<\theta<180°$$

Ángulo llano: Un ángulo llano es aquel cuya medida es igual a 180°

El $\angle{ABC}$ es un llano porque $\angle{ABC}=180°$

Ángulo de giro: El ángulo de giro es aquel cuya medida es igual a 360°. Note que al la amplitud del ángulo completa la circunferencia y los rayos se sobreponen.

$\theta$ es un angulo de giro porque $\theta=360°$

Tipos de Ángulos Según su Relación con Otros Ángulos

Los ángulos también se relacionan entre sí de maneras interesantes:

Ángulos complementarios: Dos ángulos cuya suma es 90°.
Ángulos suplementarios: Dos ángulos que suman 180°.
Ángulos consecutivos: Comparten el vértice y un lado, como piezas de un rompecabezas.
Ángulos adyacentes: Son consecutivos y suplementarios a la vez.
Ángulos opuestos por el vértice: Se forman al cruzarse dos rectas, compartiendo el vértice y teniendo lados opuestos.

Ángulos complementarios: Los ángulos complementarios son aquel par de ángulos cuya suma de sus medidas es igual a 90°, es decir, $\alpha+\beta=90°$ .

Se expresa de la siguiente manera: $\alpha$ es el complemento de $\beta$ , o bien que $\alpha$ y $\beta$ son complementarios.

Ángulos Complementarios

Ángulos suplementarios: Ángulos suplementarios son aquel par de ángulos cuya suma de sus medidas es igual a 180°, es decir, $\alpha+\beta=180°$

Se expresa de la siguiente manera: $\alpha$ es el suplemento de $\beta$ , o bien $\alpha$ y $\beta$ son suplementarios.

Ángulos suplementarios

Ángulos consecutivos: Se dice que dos ángulos son consecutivos cuando tienen el mismo vértice y un rayo en común estando los otros dos lados a un costado y al otro costado del lado en común.

En consecuencia la suma de ambos ángulos es igual a la amplitud total del ángulo; es decir $\alpha+\beta=\angle{ABD}$, el rayo común entre ambos ángulos es $\overrightarrow{BC}$

$\alpha$ y $\beta$ son consecutivos porque $\alpha+\beta=\angle{ABD}$

Ángulos adyacentes: Dos ángulos son adyacentes cuando son suplementarios y consecutivos simultáneamente.

Los ángulos $\alpha$ y $\beta$ son adyacentes

Ángulos opuestos por vértice: Dos ángulos son opuestos por vértice cuando se originan de la intersección de dos líneas rectas, y cuyos rayos son opuestos en el vértice.

También puede decirse que son los ángulos que tienen el vértice en común y los rayos de uno de los ángulos son la prolongación de los rayos del otro ángulo pero en sentido contrario. Los ángulos opuestos por vértice son iguales, es decir $\gamma=\delta$

Ángulos opuestos por vértice

La Bisectriz: El Rayo que Divide

La bisectriz es un rayo que divide un ángulo en dos ángulos iguales, como un mediador justo. Su importancia radica en su capacidad para crear simetría y equilibrio en figuras geométricas.

Definición: La bisectriz de ángulo es el rayo que parte del vértice hacia la parte interior del ángulo de tal manera que se generan dos nuevos ángulos que tienen la misma amplitud. Es decir que la bisectriz es el rayo que divide la amplitud del ángulo en dos partes iguales.

El rayo $\overrightarrow{BD}$ es bisectriz del ángulo $\angle ABC$, si y solo sí, el $\angle ABD=\angle DBC$.

$\overrightarrow{BD}$ es bisectriz de$\angle ABC$ (ángulo agudo)

$\overrightarrow{BD}$ es bisectriz del (\angle ABC\) (ángulo obtuso)

Perpendicularidad y Mediatriz: Conceptos Clave en Geometría

La perpendicularidad se refiere a dos rectas que se cruzan formando ángulos rectos. La mediatriz, por otro lado, es una recta perpendicular a un segmento que pasa por su punto medio, dividiéndolo en dos partes iguales.

Perpendicularidad

Definición: Dos rectas o segmentos son perpendiculares, si cuando intersecan entre sí forman un ángulo recto. Se utiliza el símbolo $\perp $ que significa perpendicular.

Esta definición podemos describirla de la siguiente manera:

La recta $l$ es perpendicular al segmento $\overline{AB} $, se escribe $l \perp \overline{AB} $, si el ángulo $\angle BCD = 90°$.

$l$ es perpendicular a $\overline{AB} $ porque el ángulo que forman entre ambas es recto

En consecuencia cuando dos rectas son perpendiculares estas generan cuatro ángulos rectos.

$l \perp \overline{AB} $, generando cuatro ángulos rectos.

Mediatriz

Definición: La mediatriz de un segmento es la recta o segmento perpendicular a este que pasa por su punto medio.

La recta $\overleftrightarrow{CD}$ es mediatriz del segmento $\overline{AB}$ siempre y cuando $\overline{AB} \perp \overleftrightarrow{CD} $ y $\overline{AC} = \overline{BC}$.

La recta $ \overleftrightarrow{CD} $ es la mediatriz del segmento $\overline{AB} $

Ejercicios Propuestos: Desafía tus Habilidades Geométricas

Ahora que hemos explorado los conceptos básicos de los ángulos, es hora de poner a prueba tus conocimientos con algunos ejercicios desafiantes. ¡Resuelve los problemas y demuestra tu dominio de la geometría!

Ejercicio 1.

El doble de la diferencia entre el suplemento y el complemento de un ángulo es cuatro veces la amplitud de dicho ángulo. Encontrar la medida del el suplemento del complemento de dicho ángulo.

DATOS.

1) Sea $\alpha$ un ángulo

2) $180- \alpha$ es el suplemento de $\alpha$ [Definición de suplemento: $(180- \alpha)+\alpha=180$]

3) $90 - \alpha$ es el complemento de $\alpha$ [Definición de complemento $(90- \alpha)+\alpha=90$]

Q) Hallar: $180 - (90 - \alpha) = 180 - 90 + \alpha = 90 + \alpha$

4) $2((180-\alpha)-(90-\alpha))=4\alpha$ [ Por 2) y 3) y condición del problema ]

$2(180-\alpha - 90 + \alpha)=4\alpha$

$2(90)=4\alpha$

$\alpha=45$

5) $90+\alpha=90+45=135$ [De Q) y 4 )]

Q: RESPUESTA: La medida del suplemento del complemento del ángulo es de 135°.

Ejercicio 2.

Sean los ángulos $\alpha$, $\beta$, $\gamma$ y $\delta $ ángulos consecutivos situados uno inmediatamente despues del otro en el orden mencionado, de manera tal que forman un ángulo de giro. Hallar la medida del angulo $\gamma$, si se sabe que: $\beta = \dfrac{2}{3} \alpha$; $\gamma= 4 \beta$ y $3\delta=2 \alpha$. Luego realice el gráfico correspondiente a los referidos ángulos.

RESOLUCIÓN

DATOS

1) Los ángulos $\alpha$, $\beta$, $\gamma$ y $\delta $ son ángulos consecutivos [Dato]

2) $\alpha + \beta + \gamma +\delta =360 $ [Definición de ángulo de giro ]

Q) Hallar la medida del ángulo $\gamma$

3) $\gamma= 4 \beta \Rightarrow \beta = \dfrac{ \gamma}{4} $ [Dato]

4) $\beta = \dfrac{2}{3} \alpha \Rightarrow \alpha = \dfrac{3 \beta}{2}$ [Dato]

5) $\alpha = \dfrac{3 \beta}{2}= \dfrac{3}{2}* \dfrac{\gamma}{4} \Rightarrow \alpha = \dfrac{3 \gamma}{8}$ [De 3) y 4)]

6) $3\delta=2 \alpha \Rightarrow \delta = \dfrac{2 \alpha}{3} =$ $\dfrac{2}{3}* \dfrac{3 \gamma}{8} \Rightarrow \delta = \dfrac{\gamma}{4}$ [Dato y 5)]

7) $\dfrac{3 \gamma}{8} + \dfrac{ \gamma}{4}+ \gamma + \dfrac{\gamma}{4} =360$ [Sustituir en 2) los puntos: 5), 3) y 6)]

$(\dfrac{3+2++8+2}{8})\gamma$ =360

$\dfrac{15 \gamma}{8} =360 \Rightarrow \gamma = 192 $

Q: RESPUESTA: El ángulo $\gamma$ mide 192°

Gráfico del problema 2

Ejercicio 3.

De los ángulos adyacentes $\angle ABC$ y $\angle CBD$ se trazan sus respectivas bisectrices $\overrightarrow{BM}$ y $\overrightarrow{BN}$ en ese orden. Encontrar la medida del ángulo formado por las bisectrices de los ángulos $\angle ABN$ y $\angle DBM$.

DATOS

1) $\angle ABC + \angle CBD = 180$ [Dato y definición de angulo adyacente]

2) $\overrightarrow{BM}$ es bisectriz de $\angle ABC$ [Dato]

3) $\overrightarrow{BN}$ es bisectriz de $\angle DBC$ [Dato]

4) Con estos datos construimos el grafico y asignamos una notación.

5) $2\alpha +2\beta =180 $$\Rightarrow \alpha + \beta = 90 $ [De 4) y 1)]

6) $\angle ABN = 2\alpha + \beta$ [De 4)]

7) $\angle DBM = \alpha + 2\beta$ [De 4)]

8) Construir la bisectriz $\overrightarrow{BE}$ del $\angle ABN$ [Construcción]

9) Construir la bisectriz $\overrightarrow{BF}$ del $\angle DBM$

10) El ángulo formado entre las bisectrices $\overrightarrow{BE}$ y $\overrightarrow{BF}$ de los angulos $\angle ABN$ y $\angle DBM$ es el ángulo $\theta$ [Construcción, 8), 9) y Dato]

Q: Hallar la medida del ángulo $\theta $

11) $\angle ABE + \theta + \angle CBD = 180$ [De 10), son ángulos adyacentes]

12) $2\angle ABE = \angle ABN$ [De 8), por la bisectriz]

$\Rightarrow\angle ABE = \dfrac{\angle ABN}{2}$

13) $2\angle DBF = \angle DBM$ [De 9), por la bisectriz]

$\Rightarrow \angle DBF =\dfrac{\angle DBM}{2}$

14) $\dfrac{\angle ABN}{2}+\theta+\dfrac{\angle DBM}{2}= 180$ [Sustituir 12) y 13) en 11)]

15) $\dfrac{2\alpha+\beta}{2}+\theta+\dfrac{\alpha+2\beta}{2}=180$ [Sustituir 6) y 7) en 14)]

16) $\theta=180-\dfrac{3}{2}(\alpha+\beta)$ [Simplificando 15)]

17) $\theta=180-\dfrac{3}{2}(90)=45$ [Sustituir 5) en 16)]

Q: RESPUESTA: El ángulo $\theta$ formado por las referidas bisectrices tiene una amplitud de 45°.

Conclusión

¡Felicitaciones por completar este viaje a través del mundo de los ángulos! Hemos recorrido un largo camino, desde los fundamentos hasta conceptos más avanzados. Ahora estás equipado con el conocimiento necesario para identificar, medir y clasificar ángulos, así como para resolver problemas geométricos que involucren ángulos.

Recuerda que la geometría está presente en todas partes, desde las formas de los edificios hasta los patrones de la naturaleza. ¡Sigue explorando y descubriendo las maravillas de esta fascinante disciplina

TRADUCTOR

Ángulos en Geometría: Guía Completa con Ejercicios Resueltos